Temps réel/Approches avec exécutif

Systèmes

Noyau

Fournis le strict minimum

Exemple : Noyau TR RTC

• 27 primitives
• 3 à 4 Ko

Exécutif

C'est un noyau étendu

Système d'exploitation

Un éxécutif, plus un environnement de développement convivial.

Traitement monotâche

Le programme se résume à une boucle de scrutation.

Traitement multitâches

En deux phases :

• Prise en compte des évènements
• Activation de la partie logicielle associée a l'événement

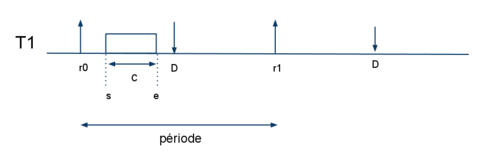
Légende

• C : durée maximale d'exécution de la tâche lorsqu'elle a le processeur pour elle tout seule
• D : délai critique, échéance, date maximale à laquelle l'exécution la tâche doit être terminée
• P : période, durée qui s'écoule entre deux requêtes successives
• s : task start
• e : end en task
• TR : temps de réponse de la tâche

TR = e - r

AUTRE SCHEMA ICI

• Laxité nominale : 5 - 2 = 3
  ie : on peut retarder au maximum l'exécution de T1 jusqu'à la date 3, après il y a une faute temporelle
• Laxité nominale résiduelle : calculée à t = 2, indique que l'on peut attendre jusqu'à la date 4 pour reprendre l'exécution de T1
• Estimation de la durée maximale d'exécution d'une tâche lorsqu'elle dispose du processeur pour elle seule, WCET (worst case execution time) = C

Etude d'un cas

Estimation de la durée maximale d’exécution d'une tâche lorsqu'elle dispose du processeur pour elle toute seule.

WCET (worst case execution time) = C

 procedure P(a,b,entier)
 début
   pour i allant de 1 jusqu'à a faire
     si (b >= 4) alors traitement X (très long)
       sinon traitement Y (moins long)
     fin si
   fin pour
 fin procédure P

Méthode d'analyse dynamique

On exécute le programme pour plusieurs jeux d'entrée a et b (paramètres d'entrée) sur une machine donnée.

Le WCET s'obtient en faisant la différence entre la date machine à la fin d'exécution et la date machine relevée en début d'exécution.

Difficulté : connaître précisément les plages de variation des paramètres d'entrée.

Méthode d'analyse statique

On transforme le programme en un problème mathématique d'optimisation linéaire

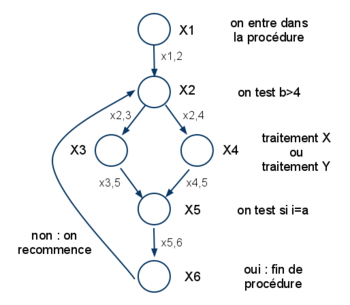
On associe au programme un graphe :

• Noeud : une suite d'instruction non conditionelles auquel on peut associer un temps d'exécution (lié à la machine)

• x : le nombre d'exécution du noeud i
• xi,j : le nombre de franchissement de l'arc entre xi et xj

Trouver le WCET reviens à : Maximiser

z = x1 t1 + x2 t2 + x3 t3 + x4 t4 + x5 t + x6 t6

Avec les contraintes

• x1 = 1 = x6
  car on entre ou on sort une fois de la proc.
• x5,2 <= 10
  car on reboucle 10 fois au max
• x2 = x1,2 + x5,2 = x2,3 + x2,4
  car on entre dans un noeud autant de fois qu'on en sort
• x4 = x2,4 = x3,5
• x5 = x2,5 + x4,5 = x5,6 + x5,2

Approches et techniques classiques

Voir le cours Système d'exploitation (ordonnancement des processus)

• Fonctionnement en temps partagé
  • Temps partagé en round-robin simple (une file)
  • Techniques des files d'attente multiples
    Favorise les processus courts, ralenti les processus longs.

Tâches périodiques indépendantes

1er cas : uniquement des tâches périodiques

• qui ne partagent pas de ressources
• non liées par des contraintes de précédence

Algorithme à priorité constante

• P = Période
• C = Durée d'exécution
• r = date de réveil

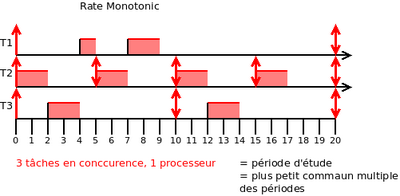
Exemple : Rate Monotonic

• Tp1 = (r0 = 0 , C = 3 , P = 20)
• Tp2 = (r0 = 0 , C = 2 , P = 5)
• Tp3 = (r0 = 0 , C = 3 , P = 10)

Condition suffisante :

Somme[i = 1 jusque n] Ci / Pi <= n ( 2^1/n - 1 )

Somme[i = 1 jusque 3] Ci / Pi = 3/20 + 2/5 + 2/10 = 0,75

3(2 ^{1/3} - 1) = 0,78

Donc les tâches sont ordonnancables

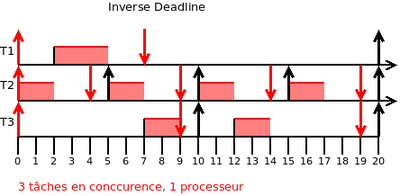
Exemple : Inverse deadline

• Tp1 = (r0 = 0 , C = 3 , D = 7 , P = 20)
• Tp2 = (r0 = 0 , C = 2 , D = 4 , P = 5)
• Tp3 = (r0 = 0 , C = 3 , D = 9 , P = 10)

= Somme[i = 1 jusque 3] Ci / Pi = 0,79

3(2 ^{1/3} - 1) = 0,78

P(Tp2) > P() ..........

Algorithme à priorité variable

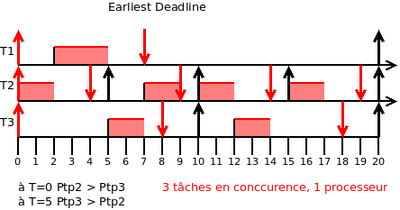
Exemple : Earliest Deadline

• Tp1 = (r0 = 0 , c = 3 , D = 7 , P = 20)
• Tp2 = (r0 = 0 , c = 2 , D = 4 , P = 5)
• Tp3 = (r0 = 0 , c = 3 , D = 8 , P = 10)

à t = 0, P(Tp2) > P(Tp3)

à t = 5, P(Tp3) > P(Tp2)

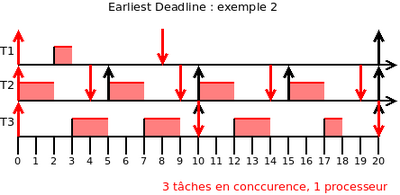
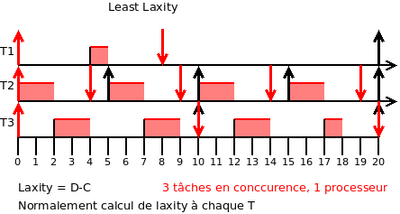
Exemple 2 : Earliest Deadline et Least Laxity

• Tp1 = (r0 = 0 , c = 1 , D = 8 , P = 20)
• Tp2 = (r0 = 0 , c = 2 , D = 4 , P = 5)
• Tp3 = (r0 = 0 , c = 4 , D = 10 , P = 10)

à t = 0

• L1 = 8 - 1 = 7
• L2 = 4 - 2 = 2
• L3 = 10 - 4 = 6

à t = 3

• L1 = 8 - 1 = 7
• L3 = 10 - 3 = 7

à t = 4

• L1 = 8 - 1 = 7
• L3 = 10 - 2 = 8

Tâches apériodiques à contraintes relatives

2ème cas : tâches périodiques + périodiques à contraintes relatives

• sans partage de ressources
• sans contrainte de précédence

Traitement d'arrière plan

Exemple

Tâches périodiques, ordonnées suivant l'algorithme "Rate Monotonic" :

• Tp1 (r0 = 0 , C = 2 , P = 5)
• Tp2 (r0 = 0 , C = 2 , P = 10)

Tâches apériodiques

• Ta3 (r0 = 4 , C = 2)
• Ta4 (r0 = 10 , C = 1)
• Ta5 (r0 = 11 , C = 2)

Serveur de tâches

Tâches périodiques, ordonnées suivant l'algorithme "Rate Monotonic" :

• Tp1 (r0 = 0 , C = 3 , P = 20)
• Tp2 (r0 = 0 , C = 2 , P = 10)
• Tp3 (r0 = 0 , C = 2 , P = 5)

Tâches périodiques

• Ta3 (r0 = 4 , C = 2)
• Ta4 (r0 = 10 , C = 1)
• Ta5 (r0 = 11 , C = 2) <-- serveur de tâches apériodiques

à t = 0, aucune tâches apériodique à servir, le programme est attribué à Tp2 (non pas à Tp3)

Tâches apériodiques à contraintes strictes

Exemple

Ordonnancement selon l'algorithme Earliest Deadline

Tâches périodiques

• Tp1 (r0 = 0 , C = 3 , D = 7 , P = 20)
• Tp2 (r0 = 0 , C = 2 , D = 4 , P = 10)
• Tp3 (r0 = 0 , C = 2 , D = 8 , P = 5)

Tâches apériodiques critiques

• Ta3 (r0 = 4 , C = 2 , D = 10)
• Ta4 (r0 = 10 , C = 1 , D = 18)
• Ta5 (r0 = 11 , C = 2 , D = 16)

Traitement des Situations de surcharge

Si on peut pas respecter tout ls échéances temporelles On favorise le traitement des tâches les plus importantes Ti(ri,ci,Di,Pi,imp) imp : Importance de la tâche. Algorithme : A une date donnée, On classe la liste des tâches actives selon leur ordre croissante d'échéance T={Ti} Pour chaque tâche \(Ti \in T\) on calcule \(LCi = Di - (\sum_{j} Cj, dj \leslant di ) \) si \(\exists LCi < 0\) alors il y a surchage.

LC = Echéchance - t - tache restante - tache precedente.